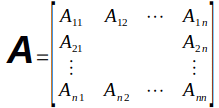Tag: Math

Writing in LibreOffice for WordPress

One of the many things that LibreOffice does exceptionally well is formatting mathematical expressions. Since I on working with matrices quite a bit in the near future, I thought it might benefit me to see write in LibreOffice.

While I can write notes for myself in LibreOffice quite easily, the question becomes: can I share them on WordPress? And if I can, will WordPress display the matrices that I have created correctly or will they be mangled?

We shall soon see.

Here is an example matrix that was given by the LibreOffice how-to pages:

It is very easy to create and put in place. It looks fantastic in LibreOffice.

Next, here is a matrix that I have created myself using a much simpler version of the formula.

Now, I am going to save this as a html file and see if I can copy and paste it into the new WordPress block editor.

End result:

It seems like it works quite well. There is a downside, though. When I saved the document from LibreOffice’s default ‘odt’ format to ‘html’ format, it exported the formulas as images. When I copied the entire html file to WordPress’s new block editor, it left blanks for each of the images that needed to be inserted. While not a perfect solution, I think that is probably my best bet for now.

Linear algebra basics

Unfortunately when I was taking linear algebra in college, I didn’t realize just how important it would later in my life. While I do remember plenty of the basics, there is also huge holes in my knowledge of linear algebra. These holes became apparent when I started doing extensive work in the area of data analysis.

It is time to correct this problem.

As a starting point, I will be using the linear algebra videos from 3blue1brown on YouTube to quickly cover the basics. These notes will be covering the first of his videos titled Vectors, what even are they? Essence of linear algebra, chapter 1 available on YouTube here.

Useful Unicode for inputting vector notation in Linux

To input Unicode into Linux, hold down the control and shift key while pressing the ‘u’ key. The ‘u’ will be underlined at that point. Then type in the four digit code for the character that you want to input. Here are the codes that I use to create vector notation in a text document:

u23a7 ⎧   u23ab ⎫
u23aa ⎪   u23aa ⎪
u23a9 ⎩   u23ad ⎭

A dot product is represented by u00b7 ·
A cross product is represented by an x.

While these codes should be useful in all operating systems, the way that they are input will differ.

Vectors are rooted at the origin of the coordinate system

While this isn’t specifically true in all cases, that is the convention that we will be using for the time being. By placing the tail of the vector at the origin of the coordinate system, that makes vector addition and scalar multiplication easy and intuitive. Later, if it becomes necessary, we can take the view of vectors that are at arbitrary places within the coordinate system.

In a two dimensional space, the origin is the point where the x-axis crosses the y-axis. This is usually designated mathematically as the point (0, 0). In a three dimensional space, it is the point where the x-axis, y-axis, and z-axis meet. In three dimensional space, it would be designated by the point (0, 0, 0).

That brings us to our first distinction in linear algebra. In linear algebra, we are working with vectors, not points. To distinguish between them. they are usually written on top of each other and surrounded by square brackets instead of curved brackets.

⎧5⎫
⎩4⎭

You can think of the numbers given in a vector as the instructions to get from the tail of the vector to the tip of the vector. The top number tells how far to move on the x-axis, the second number tells how far to move along the y-axis, and the third number (if available) tells how far to move along the z-axis.

This convention can be extended into more than three dimensions if desired.

Vector addition

To add two vectors, imagine both of them with their root at the origin. Then, imagine the second vector moving its root to the tip of the first vector while still maintaining its direction and magnitude. The resulting vector, rooted at the origin, will have its tip at the end of the second vector.

This can be expressed mathematically as follows:

⎧1⎫   ⎧3 ⎫   ⎧  1+3 ⎫   ⎧4⎫
⎩2⎭ + ⎩-1⎭ = ⎩2+(-1)⎭ = ⎩1⎭

Scaling a vector (multiplication by a number)

A scalar is a number that scales a vector. Pretty well every stand-alone number in linear algebra can be thought of as a scalar. What a scalar does is shrink, extend, and/or change directions of a vector while maintaining its origin and the line upon which it sits.

Negative numbers change the vector’s direction while positive numbers maintain the vector’s direction. The scaling is determined by the magnitude of the number. For example

  ⎧3⎫   ⎧6⎫
2·⎩1⎭ = ⎩2⎭

All you have to do is multiply each component of the vector by the scalar. That has the function of stretching (or shrinking) the vector. And if the scalar is negative, it will also flip the direction of the vector.

Covid-19 update 1: data as the United States begins to open.

As the United States begins to open from its Covid-19 shutdown, it is important to get a baseline to see how the disease progresses as the stay-at-home orders begin to wane. To create a yardstick, I will be relying on data from Johns Hopkins University available at their GitHub page [https://github.com/CSSEGISandData/COVID-19]. After I process the data, that should give a snapshot of the condition of each individual state as well as an overall view of the United States. With the snapshot in place, it will be easier to see how the infection rate changes over time.

To process the data into easily readable form, I first take the total of infections per day and spread them out through a skewed normal curve. I use a normal graph that is skewed to the left to help distribute the raw data into the most likely time that the person was actually infected instead of the time when they received a positive test result. The downside to processing the data like this is that it is a trailing indicator. In other words, it shows what the infection rate would have been about two weeks prior to the last data available. In order to help compensate for the lag in processed data, I also put the raw data into the same chart. That makes it easier to see where the data might be going over time.

Here is a graph of the United States using the data available as of the end of the day on April 28, 2020.

The “reported” data is taken directly from the data provided by Johns Hopkins University while the “normalized” data is the same data processed through normal distribution.

With the data processed this way, it is easy to see the initial growth rate as well as when it peaked and started down.

The overall downward trend for the United States is what I would expect considering that the states that had the worst outbreaks are rapidly bringing those outbreaks under control. But this doesn’t tell the entire story. As we have all seen, the picture of the United States doesn’t necessarily indicate how each individual part is doing. There are several states that are bringing their daily infections under control while there are others that are still spreading on an exponential curve. Furthermore, as each state applies its own rules to reopening, it’s quite likely that each state will diverge from the others with respect to their infection rate.

Since showing a graph of each state every time I update would be prohibitive, I will show a few that are opening early.

As you can see from the graph of Alaska, they seem to have their outbreak well in hand. Alaska never had a very big outbreak; notice the y-axis and that they are only getting about 5 infections per day. It shouldn’t take much of an effort to keep their outbreak under control.

Georgia is the next state that I want to look at. While Georgia has flattened their curve, they haven’t done much to actually reduce the number of daily infections. With between 600 and 800 daily infections, it will be easy for them to slip back into a exponential growth rate. Even if they manage to escape an exponential growth rate when they begin to return to work, 600 to 800 new cases of Covid-19 per day will serve to maintain a stress on their healthcare system.

Minnesota is trying to open their economy a little bit while still maintaining their stay-at-home order. While their daily infection rate isn’t outrageous, it doesn’t appear to have reached its peak yet.

Mississippi is another state that is trying to reopen their economy. They, too, might not have reached their peak.

Oklahoma appears to have had an initial success of reaching their peak and even starting to reduce their daily infection rate. On the other hand, Oklahoma is being fairly aggressive in reopening their businesses. This state could be the canary in the coalmine as far as whether the daily infection rates begin to clime again after the economy starts to reopen.

South Carolina is in much the same position as Oklahoma with respect to their daily infection rate and reopening strategy. Perhaps they are another canary in the coalmine.

Finally that brings us to Tennessee. While they have flattened their curve, they don’t seem to have reduced the daily infection rate. They are also being very aggressive with their reopening plans. Over the next few days, they are going to remove all stay-at-home restrictions and rely completely on social distancing to try to maintain their daily infection rates.

And that concludes the states that are leading the charge to reopen. It will be educational to see which, if any, of these states manage to keep their daily infection rate in check. The fate of these states is in the hands of their citizens. Whether they take the threat of Covid-19 seriously when they return to work or whether they end up being the first states to require a second round of stay-at-home orders remains to be seen.